Je vais donc vous parler des coordonnées du système géodésique réel, puis de comment ça se passe dans DCS. Je vais essayer de me mettre au niveau de quelqu'un qui n'y connait pas grand chose en mat.
Je n'utiliserai pas forcément les formules les plus rapides mais les plus intuitives.
Le système longitude/latitude :
Les méridiens sont des courbes qui parcourent le globe sur l'axe N/S.
Les parallèles sont des courbes qui parcourent le globe sur l'axe E/O.
Les parallèles sont perpendiculaires aux méridiens.
On repère les méridiens par l'angle qu'ils forment avec le meridien de greenwich. Le sommet de l'angle étant le centre de la terre.
On repère les parallèles par l'angle qu'ils forment avec l'équateur, placé de façon équidistante entre le pole N et le pole S.
En principe jusqu'ici vous n'avez rien appris.
Les degrés peuvent être subdivisés en 60 minutes, puis ces minutes en 60 secondes. On à donc 3600 secondes pour 1°, comme pour le système horaire.
Sur l'axe des méridiens ( donc N-S) si je me déplace de 1 minute, je parcours 1 Nm, c'était la définition du Nm.
En effet, tous les méridiens font la même longueur ou (demi)circonférence.
Si je me déplace d'un angle donné sur cette circonférence il suffit de faire le ratio : [angle° / 360°] pour trouver le ratio [Distance parcouru / Circonférence de la terre]
On a donc un simple :
Distance parcourue sur le méridien = Angle parcouru en minute sur le méridien
Sur l'axe des parallèles [E-O] c'est plus compliqué.
La parallèle ayant la plus grande circonférence est l'équateur.
Les parallèles sont plus petites au fur et à mesure que l'on s'éloigne de l'équateur et que leur numéro de baptême grandi.
Les plus petite sont ponctuelles, c'est à dire qu'elle a une circonférence égale à zero : La parallèle + 90 ( pôle Nord) et la parallèle -90 ( pôle sud).
La formule qui lie la circonférence de la parallèle avec son Numéro est :
Longueur de la parallèle = Circonférence de l'équateur * Cosinus (Numéro de la parallèle)
Pour les non matheux, Cosinus(x) est une courbe avec Cosinus ( 0 ) = 1 et Cosinus (90) = 0.
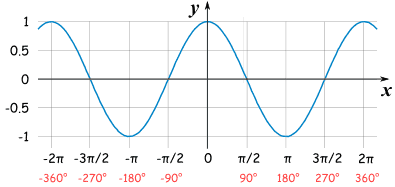
On voit bien que pour nos calcul, sur les pôles on multipliera la longueur de l'équateur par 0 et que sur l'équateur on la multipliera par 1.
Sur l'axe des parallèles (E-O), pour connaître ma distance parcourue en fonction de l'angle parcourue je dois donc faire :
Angle en minutes * Cosinus( numéro de la parallèle) = Distance parcourue en Nm sur cette parallèle
Pour DCS : C'est pour cela que la grille long/lat sur la carte f10 forme des rectangles et non des carrés. il faut 1Nm pour parcourir 1minute d'angle sur l'axe N-S, mais il ne faut que 0,67Nm pour faire 1 minute d'angle sur l'axe E-O sur la parallèle 42° N [ 1 * sinus(42°) ] .
Donc pour DCS : 1 minute sur l'axe N-S = 1Nm
1 minute sur l'axe E-O ~2/3 Nm
On vient de voir comment calculer un distance sur les axes N-S et E-O en fonction de l'angle.
On va voir comment calculer une distance qui n'est pas sur ces axes :
Les coordonnées d'un point sont en deux parties, une partie désignant la position du point sur l'axe N-S et une autre sur l'axe E-O.
Lorsque je veux calculer la distance entre deux points:
je compare la différence d'angle sur l'axe N-S et j'en déduis une distance.
Je compare la différence d'angle sur l'axe E-O et j'en déduise une autre distance.
Grace à Pythagore je trouve la distance entre les deux points:
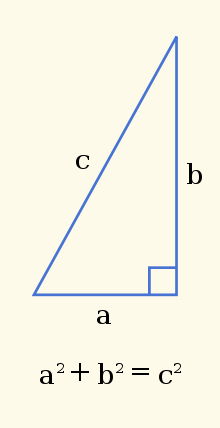
Si je remplace "a" par la distance E-O et "b" par la distance N-S, je peux trouver la distance "c".
Distance entre les deux points = RACINE ( [Distance N-S]² + [Distance E-O]² )
Calculer l'azimut entre deux points:
Si on reprend la figure :

On a déjà calculé "a", "b" et "c".
On va considéré que l'on à pas encore calculé la distance "c". On n'a donc que "a" et "b".
Notre objectif est de déterminer l'angle AC.
Si on se rappelle des cours de trigonométrie : tan = opposé / adjacent.
Pour trouver l'angleAC je fais donc :
AC = ATAN("b"/"a")
Ce qui correspond à :
Azimut = ATAN ([ Distance parcourue sur axe N-S]/[Distance parcourue sur l'axe E-O])
Comme j'ai dit, ceci est la formule simple et relativement intuitive, elle ne prend pas en compte le fait que par exemple : -90° = 270°, il faut donc l'appliquer en réfléchissant un peu. La formule complète est plus compliquée.
Toutes les formules utilisés considèrent que la terre est parfaitement sphérique, ce qui n'est pas le cas.
Un PDF de IGN à propos du calcul de distance: http://geodesie.ign.fr/contenu/fichiers ... titude.pdf
La formule pour trouver les azimuts :
azimut (point 1 -> point 2 ) =2arctan( y / [ racine ( x2+y2√) ] +x )
avec :
x=cos(lat1)∗sin(lat2)−sin(lat1)∗cos(lat2)∗cos(long2−long1)
y=sin(long2−long1)∗cos(lat2)